Triangulierte Kategorie - Triangulated category

In der Mathematik ist eine triangulierte Kategorie eine Kategorie mit der zusätzlichen Struktur eines "Übersetzungsfunktors" und einer Klasse von "exakten Dreiecken". Prominente Beispiele sind die abgeleitete Kategorie einer abelschen Kategorie sowie die Kategorie der stabilen Homotopie . Die genauen Dreiecken verallgemeinern die kurzen exakten Sequenzen in einer abelschen Kategorie sowie Fasersequenzen und cofiber Sequenzen in der Topologie.

Ein Großteil der homologischen Algebra wird durch die Sprache der triangulierten Kategorien geklärt und erweitert. Ein wichtiges Beispiel ist die Theorie der Garbenkohomologie . In den 1960er Jahren bestand eine typische Verwendung von triangulierten Kategorien darin, die Eigenschaften von Garben auf einem Raum X auf Komplexe von Garben zu erweitern, die als Objekte der abgeleiteten Kategorie von Garben auf X angesehen wurden . In jüngerer Zeit sind triangulierte Kategorien zu eigenständigen Objekten von Interesse geworden. Viele Äquivalenzen zwischen triangulierten Kategorien unterschiedlicher Herkunft wurden bewiesen oder vermutet. Zum Beispiel sagt die Vermutung der homologischen Spiegelsymmetrie voraus, dass die abgeleitete Kategorie einer Calabi-Yau-Mannigfaltigkeit der Fukaya-Kategorie ihrer symplektischen Mannigfaltigkeit "Spiegel" entspricht .

Geschichte

Triangulierte Kategorien wurden unabhängig voneinander von Dieter Puppe (1962) und Jean-Louis Verdier (1963) eingeführt, obwohl Puppes Axiome weniger vollständig waren (ohne das oktaedrische Axiom (TR 4)). Puppe war von der Kategorie der stabilen Homotopie motiviert. Verdiers Schlüsselbeispiel war die abgeleitete Kategorie einer abelschen Kategorie, die er auch definierte und Ideen von Alexander Grothendieck entwickelte . Die frühen Anwendungen abgeleiteter Kategorien umfassten kohärente Dualität und Verdier-Dualität , die die Poincaré-Dualität auf singuläre Räume erweitert.

Definition

Eine Verschiebung oder Translation Funktors auf eine Kategorie D ist ein additives automorphism (oder für einige Autoren eine auto- Äquivalenz ) von D zu D . Es ist üblich, für ganze Zahlen n zu schreiben . ${\ displaystyle \ Sigma}$${\ displaystyle X [n] = \ Sigma ^ {n} X}$

Ein Dreieck ( X , Y , Z , u , v , w ) besteht aus drei Gegenständen X , Y und Z , zusammen mit morphisms , und . Dreiecke werden im Allgemeinen in der enträtselten Form geschrieben: ${\ displaystyle u \ Doppelpunkt X \ bis Y}$${\ displaystyle v \ Doppelpunkt Y \ bis Z}$${\ displaystyle w \ Doppelpunkt Z \ bis X [1]}$

${\ displaystyle X {\ xrightarrow {{} \ atop u}} Y {\ xrightarrow {{} \ atop v}} Z {\ xrightarrow {{} \ atop w}} X [1],}$

oder

${\ displaystyle X {\ xrightarrow {{} \ atop u}} Y {\ xrightarrow {{} \ atop v}} Z {\ xrightarrow {{} \ atop w}}}$

kurz gesagt.

Eine triangulierte Kategorie ist eine additive Kategorie D mit einem Übersetzungsfunktor und einer Klasse von Dreiecken, die als exakte Dreiecke (oder unterscheidbare Dreiecke ) bezeichnet werden und die folgenden Eigenschaften (TR 1), (TR 2), (TR 3) und (TR 4) erfüllen. . (Diese Axiome sind nicht völlig unabhängig, da (TR 3) von den anderen abgeleitet werden kann.)

TR 1

• Für jedes Objekt X ist das folgende Dreieck genau:

${\ displaystyle X {\ overset {\ text {id}} {\ to}} X \ to 0 \ to X [1]}$

• Für jeden Morphismus gibt es ein Objekt Z ( Kegel oder Cofaser des Morphismus u genannt ), das in ein genaues Dreieck passt ${\ displaystyle u \ Doppelpunkt X \ bis Y}$

${\ displaystyle X {\ xrightarrow {{} \ atop u}} Y \ bis Z \ bis X [1]}$

Der Name "Kegel" stammt vom Kegel einer Karte von Kettenkomplexen , die wiederum vom Kartierungskegel in der Topologie inspiriert wurde . Aus den anderen Axiomen folgt, dass ein genaues Dreieck (und insbesondere das Objekt Z ) durch den Morphismus bis zum Isomorphismus bestimmt wird , wenn auch nicht immer bis zu einem eindeutigen Isomorphismus. ${\ displaystyle X \ bis Y}$

• Jedes Dreieck, das zu einem exakten Dreieck isomorph ist, ist exakt. Dies bedeutet, dass wenn

${\ displaystyle X {\ xrightarrow {{} \ atop u}} Y {\ xrightarrow {{} \ atop v}} Z {\ xrightarrow {{} \ atop w}} X [1]}$

ein exaktes Dreieck ist, und , , und sind Isomorphien, dann ${\ displaystyle f \ Doppelpunkt X \ bis X '}$${\ displaystyle g \ Doppelpunkt Y \ bis Y '}$${\ displaystyle h \ Doppelpunkt Z \ bis Z '}$

${\ displaystyle X '{\ xrightarrow {guf ^ {- 1}}} Y' {\ xrightarrow {hvg ^ {- 1}}} Z '{\ xrightarrow {f [1] wh ^ {- 1}}} X. '[1]}$

ist auch ein genaues Dreieck.

TR 2

Wenn

${\ displaystyle X {\ xrightarrow {{} \ atop u}} Y {\ xrightarrow {{} \ atop v}} Z {\ xrightarrow {{} \ atop w}} X [1]}$

ist ein genaues Dreieck, dann sind es auch die beiden gedrehten Dreiecke

${\ displaystyle Y {\ xrightarrow {{} \ atop v}} Z {\ xrightarrow {{} \ atop w}} X [1] {\ xrightarrow {-u [1]}} Y [1]}$

und

${\ displaystyle Z [-1] {\ xrightarrow {-w [-1]}} X {\ xrightarrow {{} \ atop u}} Y {\ xrightarrow {{} \ atop v}} Z. \}$

Im Hinblick auf das letzte Dreieck wird das Objekt Z [−1] als Faser des Morphismus bezeichnet . ${\ displaystyle X \ bis Y}$

Das zweite gedrehte Dreieck hat eine komplexere Form, wenn und sind keine Isomorphismen, sondern nur gegenseitig inverse Äquivalenzen von Kategorien, da es sich um einen Morphismus von bis handelt , und um einen Morphismus zu erhalten , muss man mit der natürlichen Transformation komponieren . Dies führt zu komplexen Fragen über mögliche Axiome, die man den natürlichen Transformationen auferlegen muss, und in ein Paar inverser Äquivalenzen. Aufgrund dieses Problems ist die Annahme, dass und zueinander inverse Isomorphismen sind, die übliche Wahl bei der Definition einer triangulierten Kategorie. ${\ displaystyle [1]}$${\ displaystyle [-1]}$${\ displaystyle -w [-1]}$${\ displaystyle Z [-1]}$${\ displaystyle (X [1]) [- 1]}$${\ displaystyle [X]}$${\ displaystyle (X [1]) [- 1] {\ xrightarrow {}} X}$${\ displaystyle [1]}$${\ displaystyle [-1]}$${\ displaystyle [1]}$${\ displaystyle [-1]}$

TR 3

Bei zwei exakten Dreiecken und einer Karte zwischen den ersten Morphismen in jedem Dreieck gibt es einen Morphismus zwischen den dritten Objekten in jedem der beiden Dreiecke, der alles pendeln lässt . Das heißt, in dem folgenden Diagramm (wobei die beiden Zeilen exakte Dreiecke sind und f und g Morphismen sind, so dass gu = u'f ) gibt es eine Karte h (nicht unbedingt eindeutig), die alle Quadrate pendeln lässt:

TR 4: Das oktaedrische Axiom

Lass und sei Morphismus und betrachte den zusammengesetzten Morphismus . Bilden Sie für jeden dieser drei Morphismen gemäß TR 1 exakte Dreiecke. Das oktaedrische Axiom besagt (ungefähr), dass die drei Abbildungskegel zu den Eckpunkten eines exakten Dreiecks gemacht werden können, so dass "alles pendelt". ${\ displaystyle u \ Doppelpunkt X \ bis Y}$${\ displaystyle v \ Doppelpunkt Y \ bis Z}$${\ displaystyle vu \ Doppelpunkt X \ bis Z}$

Genauer gesagt, mit genauen Dreiecken

${\ displaystyle X {\ xrightarrow {u \,}} Y {\ xrightarrow {j}} Z '{\ xrightarrow {k}} X [1]}$

${\ displaystyle Y {\ xrightarrow {v \,}} Z {\ xrightarrow {l}} X '{\ xrightarrow {i}} Y [1]}$

${\ displaystyle X {\ xrightarrow {{} \ atop vu}} Z {\ xrightarrow {m}} Y '{\ xrightarrow {n}} X [1]}$ ,

Es gibt ein genaues Dreieck

${\ displaystyle Z '{\ xrightarrow {f}} Y' {\ xrightarrow {g}} X '{\ xrightarrow {h}} Z' [1]}$

so dass

${\ Anzeigestil l = gm, \ quad k = nf, \ quad h = j [1] i, \ quad ig = u [1] n, \ quad fj = mv.}$

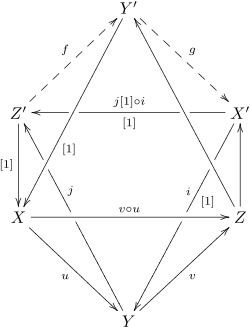
Dieses Axiom wird als "oktaedrisches Axiom" bezeichnet, da durch Zeichnen aller Objekte und Morphismen das Skelett eines Oktaeders erhalten wird , von denen vier Gesichter exakte Dreiecke sind. Die Präsentation hier ist Verdiers eigene und erscheint mit oktaedrischem Diagramm in (Hartshorne  1966 ). Im folgenden Diagramm sind u und v die angegebenen Morphismen, und die grundierten Buchstaben sind die Kegel verschiedener Karten (so gewählt, dass jedes exakte Dreieck einen X- , einen Y- und einen Z- Buchstaben hat). Verschiedene Pfeile wurden mit [1] markiert, um anzuzeigen, dass sie "Grad 1" haben; zB ist die Abbildung von Z 'nach X tatsächlich von Z ' nach X [1]. Das oktaedrische Axiom behauptet dann die Existenz von Karten f und g, die ein genaues Dreieck bilden, und so dass f und g kommutative Dreiecke in den anderen Flächen bilden, die sie enthalten:

Zwei verschiedene Bilder erscheinen in (Beilinson, Bernstein & Deligne  1982 ) (Gelfand und Manin ( 2006 ) präsentieren auch das erste). Die erste zeigt die obere und untere Pyramide des obigen Oktaeders und behauptet, dass man bei einer unteren Pyramide eine obere Pyramide ausfüllen kann, so dass die beiden Pfade von Y nach Y 'und von Y ' nach Y gleich sind (diese Bedingung) wird, vielleicht fälschlicherweise, in Hartshornes Präsentation weggelassen). Die mit + gekennzeichneten Dreiecke sind kommutativ und die mit "d" gekennzeichneten sind genau:

Das zweite Diagramm ist eine innovativere Darstellung. Genaue Dreiecke werden linear dargestellt, und das Diagramm unterstreicht die Tatsache, dass die vier Dreiecke im "Oktaeder" durch eine Reihe von Karten von Dreiecken verbunden sind, wobei drei Dreiecke (nämlich diejenigen, die die Morphismen von X nach Y vervollständigen , von Y nach Z) und von X bis Z ) gegeben sind und die Existenz des vierten behauptet wird. Man geht zwischen den ersten beiden durch "Schwenken" um X , zum dritten durch Schwenken um Z und zum vierten durch Schwenken um X '. Alle Einschlüsse in diesem Diagramm sind kommutativ (sowohl Trigonen als auch das Quadrat), aber das andere kommutative Quadrat, das die Gleichheit der beiden Pfade von Y 'nach Y ausdrückt , ist nicht ersichtlich. Alle Pfeile, die "von der Kante" zeigen, haben Grad 1:

Dieses letzte Diagramm zeigt auch eine nützliche intuitive Interpretation des oktaedrischen Axioms. In triangulierte Kategorien, spielen Dreiecken , die Rolle der exakten Sequenzen, und so ist es sinnvoll diese Objekte zu denken , als „Quotienten“, und . In diesen Begriffen drückt sich die Existenz des letzten Dreiecks einerseits aus ${\ displaystyle Z '= Y / X}$${\ displaystyle Y '= Z / X}$

${\ displaystyle X '= Z / Y \}$ (schaut auf das Dreieck  ) und ${\ displaystyle Y \ to Z \ to X '\ to}$

${\ displaystyle X '= Y' / Z '}$ (schaut auf das Dreieck  ). ${\ displaystyle Z '\ bis Y' \ bis X '\ bis}$

Zusammengenommen behauptet das oktaedrische Axiom den "dritten Isomorphismus-Satz":

${\ Anzeigestil (Z / X) / (Y / X) \ cong Z / Y.}$

Wenn die triangulierte Kategorie die abgeleitete Kategorie D ( A ) einer abelschen Kategorie A ist und X , Y , Z Objekte von A sind, die als in Grad 0 konzentrierte Komplexe angesehen werden, und die Karten und Monomorphismen in A sind , dann die Kegel dieser morphisms in D ( A ) ist tatsächlich isomorph zu den Quotienten oben in A . ${\ displaystyle X \ bis Y}$${\ displaystyle Y \ bis Z}$

Schließlich formuliert Neeman ( 2001 ) das oktaedrische Axiom unter Verwendung eines zweidimensionalen kommutativen Diagramms mit 4 Zeilen und 4 Spalten. Beilinson, Bernstein und Deligne ( 1982 ) geben ebenfalls Verallgemeinerungen des oktaedrischen Axioms.

Eigenschaften

Hier sind einige einfache Folgen der Axiome für eine triangulierte Kategorie D .

• Gegeben ein genaues Dreieck

${\ displaystyle X {\ xrightarrow {{} \ atop u}} Y {\ xrightarrow {{} \ atop v}} Z {\ xrightarrow {{} \ atop w}} X [1]}$

in D ist die Zusammensetzung von zwei aufeinanderfolgenden Morphismen Null. Das heißt, vu = 0, wv = 0, u [1] w = 0 und so weiter.

• Bei einem gegebenen Morphismus garantiert TR 1 die Existenz eines Kegels Z, der ein genaues Dreieck vervollständigt. Zwei beliebige Kegel von u sind isomorph, aber der Isomorphismus ist nicht immer eindeutig bestimmt. ${\ displaystyle u \ Doppelpunkt X \ bis Y}$

• Jeder Monomorphismus in D ist die Aufnahme eines direkten Summanden , und jeder Epimorphismus ist eine Projektion . Ein verwandter Punkt ist, dass man nicht über "Injektivität" oder "Surjektivität" für Morphismen in einer triangulierten Kategorie sprechen sollte. Jeder Morphismus , der kein Isomorphismus ist, hat einen "Kokernel" Z ungleich Null (was bedeutet, dass es ein genaues Dreieck gibt ) und auch einen "Kernel" ungleich Null, nämlich Z [−1]. ${\ displaystyle X \ bis X \ oplus Y}$${\ displaystyle X \ oplus Y \ to X}$${\ displaystyle X \ bis Y}$${\ displaystyle X \ bis Y \ bis Z \ bis X [1]}$

Nichtfunktionalität der Kegelkonstruktion

Eine der technischen Komplikationen bei triangulierten Kategorien ist die Tatsache, dass die Kegelkonstruktion nicht funktional ist. Zum Beispiel mit einem Ring und der Teilkarte der unterscheidbaren Dreiecke ${\ displaystyle R}$

${\ displaystyle {\ begin {matrix} R & \ to & 0 & \ to & R [+1] & \ to \\\ downarrow && \ downarrow &&& \\ 0 & \ to & R [+1] & \ to & R [+1] & \ to \ end {matrix}}}$

In gibt es zwei Karten, die dieses Diagramm vervollständigen. Dies kann die Identitätskarte oder die Nullkarte sein ${\ displaystyle D ^ {b} (R)}$

${\ displaystyle {\ begin {align} {\ text {id}}: & R [+1] \ bis R [+1] \\ 0: & R [+1] \ bis R [+1] \ end {align} }}$

beide sind kommutativ. Die Tatsache, dass zwei Karten existieren, ist ein Schatten der Tatsache, dass eine triangulierte Kategorie ein Werkzeug ist, das Homotopie-Grenzen und Colimit codiert . Eine Lösung für dieses Problem wurde von Grothendieck vorgeschlagen, bei der nicht nur die abgeleitete Kategorie, sondern auch die abgeleitete Kategorie von Diagrammen für diese Kategorie berücksichtigt wird. Ein solches Objekt wird als Derivator bezeichnet .

Beispiele

Gibt es bessere Axiome?

Einige Experten vermuten ^{S. 190} (siehe zum Beispiel (Gelfand & Manin  2006 , Einführung, Kapitel IV)), dass triangulierte Kategorien nicht wirklich das "richtige" Konzept sind. Der wesentliche Grund ist, dass der Kegel eines Morphismus nur bis zu einem nicht eindeutigen Isomorphismus einzigartig ist. Insbesondere hat der Kegel eines morphism im allgemeinen nicht abhängig functorially auf der morphism ( man beachte die Uneindeutigkeit in Axiom (TR 3), zum Beispiel). Diese Nicht-Eindeutigkeit ist eine potenzielle Fehlerquelle. Die Axiome funktionieren jedoch in der Praxis angemessen, und es gibt viel Literatur, die sich mit ihrem Studium befasst.

Derivatoren

Ein alternativer Vorschlag ist die Theorie der Derivate, die Grothendieck in den 80er Jahren ^{S. 191} in Pursuing Stacks vorgeschlagen und später in den 90er Jahren in seinem Manuskript zu diesem Thema entwickelt hat. Im Wesentlichen handelt es sich hierbei um ein System von Homotopiekategorien, die durch die Diagrammkategorien für eine Kategorie mit einer Klasse schwacher Äquivalenzen angegeben werden . Diese Kategorien werden dann durch die Morphismen von Diagrammen in Beziehung gesetzt . Dieser Formalismus hat den Vorteil, dass die Homotopie-Grenzen und -Kolimiten wiederhergestellt werden können, was die Kegelkonstruktion ersetzt. ${\ displaystyle I \ to M}$${\ displaystyle (M, W)}$${\ displaystyle I \ to J}$

Stabile ∞-Kategorien

Eine andere Alternative ist die Theorie der stabilen ∞-Kategorien . Die Homotopiekategorie einer stabilen ∞-Kategorie wird kanonisch trianguliert, und darüber hinaus werden Mapping-Kegel im Wesentlichen einzigartig (im präzisen homotopischen Sinne). Darüber hinaus codiert eine stabile ∞-Kategorie natürlich eine ganze Hierarchie von Kompatibilitäten für ihre Homotopiekategorie, an deren Ende sich das oktaedrische Axiom befindet. Daher ist es strikt stärker, die Daten einer stabilen ∞-Kategorie anzugeben, als die Daten einer Triangulation ihrer Homotopiekategorie. Nahezu alle triangulierten Kategorien, die in der Praxis entstehen, stammen aus stabilen ∞-Kategorien. Eine ähnliche (aber speziellere) Anreicherung von triangulierten Kategorien ist der Begriff einer dg-Kategorie .

In mancher Hinsicht funktionieren stabile ∞-Kategorien oder dg-Kategorien besser als triangulierte Kategorien. Ein Beispiel ist die Vorstellung eines exakten Funktors zwischen triangulierten Kategorien, die unten diskutiert wird. Für eine glatte projektive Sorte X über ein Feld k stammt die begrenzte abgeleitete Kategorie kohärenter Garben auf natürliche Weise aus einer dg-Kategorie. Bei den Sorten X und Y stammt jeder Funktor von der dg-Kategorie von X bis zu der von Y aus einem Garbenkomplex, der durch die Fourier-Mukai-Transformation entstanden ist . Im Gegensatz dazu gibt es ein Beispiel für einen exakten Funktor von bis , der nicht aus einem Komplex von Garben stammt . In Anbetracht dieses Beispiels scheint der "richtige" Begriff eines Morphismus zwischen triangulierten Kategorien einer zu sein, der aus einem Morphismus zugrunde liegender dg-Kategorien (oder stabiler ∞-Kategorien) stammt. ${\ displaystyle {\ text {D}} ^ {\ text {b}} (X)}$${\ displaystyle X \ times Y}$${\ displaystyle {\ text {D}} ^ {\ text {b}} (X)}$${\ displaystyle {\ text {D}} ^ {\ text {b}} (Y)}$${\ displaystyle X \ times Y}$

Ein weiterer Vorteil stabiler ∞-Kategorien oder dg-Kategorien gegenüber triangulierten Kategorien zeigt sich in der algebraischen K-Theorie . Man kann die algebraische K-Theorie einer stabilen ∞-Kategorie oder dg-Kategorie C definieren und eine Folge von abelschen Gruppen für ganze Zahlen i angeben . Die Gruppe hat eine einfache Beschreibung in Bezug auf die triangulierte Kategorie, die C zugeordnet ist . Ein Beispiel zeigt jedoch, dass die höheren K-Gruppen einer dg-Kategorie nicht immer durch die zugehörige triangulierte Kategorie bestimmt werden. Somit hat eine triangulierte Kategorie eine genau definierte Gruppe, im Allgemeinen jedoch keine höheren K-Gruppen. ${\ displaystyle K_ {i} (C)}$${\ displaystyle K_ {0} (C)}$${\ displaystyle K_ {0}}$

Andererseits ist die Theorie der triangulierten Kategorien einfacher als die Theorie der stabilen ∞-Kategorien oder dg-Kategorien, und in vielen Anwendungen ist die triangulierte Struktur ausreichend. Ein Beispiel ist der Beweis der Bloch-Kato-Vermutung , bei der viele Berechnungen auf der Ebene triangulierter Kategorien durchgeführt wurden und die zusätzliche Struktur von ∞-Kategorien oder dg-Kategorien nicht erforderlich war.

Kohomologie in triangulierten Kategorien

Triangulierte Kategorien lassen einen Begriff der Kohomologie zu, und jede triangulierte Kategorie verfügt über ein großes Angebot an kohomologischen Funktoren. Ein kohomologischer Funktor F von einer triangulierten Kategorie D zu einer abelschen Kategorie A ist ein Funktor, so dass für jedes exakte Dreieck

${\ displaystyle X \ bis Y \ bis Z \ bis X [1], \}$

Die Reihenfolge in A ist genau. Da ein genaues Dreieck eine unendliche Folge von exakten Dreiecken in beide Richtungen bestimmt, ${\ Anzeigestil F (X) \ bis F (Y) \ bis F (Z)}$

${\ displaystyle \ cdots \ bis Z [-1] \ bis X \ bis Y \ bis Z \ bis X [1] \ bis \ cdots, \}$

Ein kohomologischer Funktor F gibt tatsächlich eine lange exakte Sequenz in der abelschen Kategorie A an :

${\ displaystyle \ cdots \ zu F (Z [-1]) \ zu F (X) \ zu F (Y) \ zu F (Z) \ zu F (X [1]) \ zu \ cdots. \}$

Ein Schlüsselbeispiel ist: Für jedes Objekt B in einer triangulierten Kategorie D sind die Funktoren und kohomologisch mit Werten in der Kategorie der abelschen Gruppen . (Um genau zu sein, ist letzterer ein kontravarianter Funktor , der als Funktor in der entgegengesetzten Kategorie von D betrachtet werden kann .) Das heißt, ein genaues Dreieck bestimmt zwei lange exakte Sequenzen abelscher Gruppen: ${\ displaystyle \ operatorname {Hom} (B, {\ text {-}})}$${\ displaystyle \ operatorname {Hom} ({\ text {-}}, B)}$${\ displaystyle X \ bis Y \ bis Z \ bis X [1]}$

${\ displaystyle \ cdots \ to \ operatorname {Hom} (B, X [i]) \ to \ operatorname {Hom} (B, Y [i]) \ to \ operatorname {Hom} (B, Z [i]) \ to \ operatorname {Hom} (B, X [i + 1]) \ to \ cdots}$

und

${\ displaystyle \ cdots \ to \ operatorname {Hom} (Z, B [i]) \ to \ operatorname {Hom} (Y, B [i]) \ to \ operatorname {Hom} (X, B [i]) \ to \ operatorname {Hom} (Z, B [i + 1]) \ to \ cdots.}$

Für bestimmte triangulierte Kategorien ergeben diese exakten Sequenzen viele der wichtigen exakten Sequenzen in der Garbenkohomologie, Gruppenkohomologie und anderen Bereichen der Mathematik.

Man kann auch die Notation verwenden

${\ displaystyle \ operatorname {Ext} ^ {i} (B, X) = \ operatorname {Hom} (B, X [i])}$

Verallgemeinern Sie für Ganzzahlen i den Ext-Funktor in einer abelschen Kategorie. In dieser Notation würde die erste exakte Sequenz oben geschrieben werden:

${\ displaystyle \ cdots \ to \ operatorname {Ext} ^ {i} (B, X) \ to \ operatorname {Ext} ^ {i} (B, Y) \ to \ operatorname {Ext} ^ {i} (B. , Z) \ to \ operatorname {Ext} ^ {i + 1} (B, X) \ to \ cdots. \}$

Für eine abelian Kategorie A , ein anderes einfaches Beispiel einer kohomologische Funktors auf der abgeleiteten Klasse D ( A ) sendet eine komplexen X an das Objekt in A . Das heißt, ein genaues Dreieck in D ( A ) bestimmt eine lange exakte Folge in A : ${\ displaystyle H ^ {0} (X)}$${\ displaystyle X \ bis Y \ bis Z \ bis X [1]}$

${\ displaystyle \ cdots \ zu H ^ {i} (X) \ zu H ^ {i} (Y) \ zu H ^ {i} (Z) \ zu H ^ {i + 1} (X) \ zu \ cdots,}$

damit . ${\ displaystyle H ^ {0} (X [i]) \ cong H ^ {i} (X)}$

Genaue Funktoren und Äquivalenzen

Ein exakter Funktor (auch Triangulationsfunktor genannt ) von einer Triangulationskategorie D zu einer Triangulationskategorie E ist ein additiver Funktor , der lose gesagt mit der Übersetzung pendelt und exakte Dreiecke an exakte Dreiecke sendet. ${\ displaystyle F \ Doppelpunkt D \ bis E}$

Genauer gesagt, ein exakter Funktor weist einen natürlichen Isomorphismus auf (wobei der erste den Übersetzungsfunktor von D und der zweite den Übersetzungsfunktor von E bezeichnet ), so dass wann immer ${\ displaystyle \ eta \ Doppelpunkt F \ Sigma \ bis \ Sigma F}$${\ displaystyle \ Sigma}$${\ displaystyle \ Sigma}$

${\ displaystyle X {\ xrightarrow {{} \ atop u}} Y {\ xrightarrow {{} \ atop v}} Z {\ xrightarrow {{} \ atop w}} X [1]}$

ist ein genaues Dreieck in D ,

${\ displaystyle F (X) {\ xrightarrow {F (u)}} F (Y) {\ xrightarrow {F (v)}} F (Z) {\ xrightarrow {\ eta _ {X} F (w)} } F (X) [1]}$

ist ein exaktes Dreieck in E .

Eine Äquivalenz von triangulierten Kategorien ist ein exakter Funktor , der auch eine Äquivalenz von Kategorien ist . In diesem Fall gibt es einen exakten Funktor, so dass FG und GF natürlich isomorph zu den jeweiligen Identitätsfunktoren sind. ${\ displaystyle F \ Doppelpunkt D \ bis E}$${\ displaystyle G \ Doppelpunkt E \ bis D}$

Kompakt erzeugte triangulierte Kategorien

Sei D eine triangulierte Kategorie, so dass in D direkte Summen existieren, die durch eine beliebige Menge (nicht unbedingt endlich) indiziert sind . Ein Objekt X in D heißt kompakt, wenn der Funktor mit direkten Summen pendelt. Explizit bedeutet dies, dass für jede Familie von Objekten in D, die durch eine Menge S indiziert sind , der natürliche Homomorphismus abelscher Gruppen ein Isomorphismus ist. Dies unterscheidet sich von der allgemeinen Vorstellung eines kompakten Objekts in der Kategorietheorie, die alle Colimits und nicht nur Nebenprodukte umfasst. ${\ displaystyle {\ text {Hom}} _ {D} (X, {\ text {-}})}$${\ displaystyle Y_ {i}}$${\ displaystyle \ oplus _ {i \ in S} \ mathrm {Hom} _ {D} (X, Y_ {i}) \ bis \ mathrm {Hom} _ {D} (X, \ oplus _ {i \ in S} Y_ {i})}$

Beispielsweise ist ein kompaktes Objekt in der Kategorie der stabilen Homotopie ein endliches Spektrum. Ein kompaktes Objekt in der abgeleiteten Kategorie eines Rings oder in der quasi kohärenten abgeleiteten Kategorie eines Schemas ist ein perfekter Komplex . Im Fall einer glatten projektiven Sorte X über ein Feld kann die Kategorie Perf ( X ) perfekter Komplexe auch als die begrenzte abgeleitete Kategorie kohärenter Garben angesehen werden . ${\ displaystyle h {\ cal {S}}}$${\ displaystyle D _ {\ text {koh}} ^ {\ text {b}} (X)}$

Eine triangulierte Kategorie D wird kompakt erzeugt, wenn

• D hat willkürliche (nicht notwendigerweise endliche) direkte Summen;
• Es gibt eine Menge S von kompakten Objekten in D, so dass für jedes Nicht-Null-Objekt X in D ein Objekt Y in S mit einer Nicht-Null-Abbildung für eine ganze Zahl n vorhanden ist . ${\ displaystyle Y [n] \ to X}$

Viele natürlich vorkommende "große" triangulierte Kategorien werden kompakt erzeugt:

• Die abgeleitete Kategorie von Modulen über einen Ring R wird kompakt von einem Objekt, dem R- Modul R, erzeugt .
• Die quasi-kohärent abgeleitete Kategorie eines quasi-kompakten quasi-getrennten Schemas wird kompakt von einem Objekt erzeugt.
• Die stabile Homotopiekategorie wird kompakt von einem Objekt, dem Kugelspektrum, erzeugt . ${\ displaystyle S ^ {0}}$

Amnon Neeman verallgemeinerte den Brown-Repräsentabilitätssatz wie folgt auf jede kompakt erzeugte triangulierte Kategorie. Sei D eine kompakt erzeugte triangulierte Kategorie, ein kohomologischer Funktor, der Nebenprodukte zu Produkten bringt. Dann ist H darstellbar. (Das heißt, es gibt ein Objekt W von D, so dass für alle X. ) Für eine andere Version sei D eine kompakt erzeugte triangulierte Kategorie, T eine beliebige triangulierte Kategorie. Wenn ein exakter Funktor Nebenprodukte an Nebenprodukte sendet, hat F einen richtigen Zusatz . ${\ displaystyle H \ Doppelpunkt D ^ {\ text {op}} \ bis {\ text {Ab}}}$${\ displaystyle H (X) \ cong {\ text {Hom}} (X, W)}$${\ displaystyle F \ Doppelpunkt D \ bis T}$

Der Brown-Repräsentabilitätssatz kann verwendet werden, um verschiedene Funktoren zwischen triangulierten Kategorien zu definieren. Insbesondere verwendete Neeman es, um die Konstruktion des außergewöhnlichen inversen Bildfunktors für einen Morphismus f von Schemata , das zentrale Merkmal der kohärenten Dualitätstheorie, zu vereinfachen und zu verallgemeinern . ${\ displaystyle f ^ {!}}$

t-Strukturen

Für jede abelsche Kategorie A ist die abgeleitete Kategorie D ( A ) eine triangulierte Kategorie, die A als vollständige Unterkategorie enthält (die Komplexe sind in Grad Null konzentriert). Verschiedene abelsche Kategorien können äquivalente abgeleitete Kategorien haben, so dass es nicht immer möglich ist, A aus D ( A ) als triangulierte Kategorie zu rekonstruieren .

Alexander Beilinson , Joseph Bernstein und Pierre Deligne beschrieb diese Situation durch die Vorstellung von einer T-Struktur auf einer triangulierten Kategorie D . Eine t-Struktur auf D bestimmt eine abelsche Kategorie innerhalb von D , und unterschiedliche t-Strukturen auf D können unterschiedliche abelsche Kategorien ergeben.

Lokalisierung und dicke Unterkategorien

Sei D eine triangulierte Kategorie mit beliebigen direkten Summen. Eine lokalisierende Unterkategorie von D ist eine streng vollständige triangulierte Unterkategorie, die unter beliebigen direkten Summen geschlossen wird. Um den Namen zu erklären: Wenn ein lokalisierende Subkategorie S eine kompakt erzeugt triangulierter Kategorie D durch eine Reihe von Objekten erzeugt wird, dann gibt es eine Bousfield Lokalisierung Funktors mit Kernel S . (Das heißt, für jedes Objekt X in D gibt es ein genaues Dreieck mit Y in S und LX im rechten Orthogonal .) Diese Konstruktion umfasst beispielsweise die Lokalisierung eines Spektrums bei einer Primzahl oder die Einschränkung aus einem Komplex von Garben auf einem Raum zu einer offenen Teilmenge. ${\ displaystyle L \ Doppelpunkt D \ bis D}$${\ displaystyle Y \ bis X \ bis LX \ bis Y [1]}$ ${\ displaystyle S ^ {\ perp}}$

Ein paralleler Begriff ist für "kleine" triangulierte Kategorien relevanter: Eine dicke Unterkategorie einer triangulierten Kategorie C ist eine streng vollständige triangulierte Unterkategorie, die unter direkten Summanden geschlossen wird. (Wenn C ist idempotent-vollständig , ist eine Unterkategorie dick , wenn und nur wenn es auch idempotent-vollständig ist.) Eine lokalisierenden Subkategorie dick ist. Wenn also S eine lokalisierende Unterkategorie einer triangulierten Kategorie D ist , dann ist der Schnittpunkt von S mit der Unterkategorie kompakter Objekte eine dicke Unterkategorie von . ${\ displaystyle D ^ {\ text {c}}}$${\ displaystyle D ^ {\ text {c}}}$

Zum Beispiel beschrieb Devinatz- Hopkins- Smith alle dicken Unterkategorien der triangulierten Kategorie endlicher Spektren im Sinne der Morava-K-Theorie . Die lokalisierenden Unterkategorien der gesamten Kategorie der stabilen Homotopie wurden nicht klassifiziert.

Siehe auch

• Fourier-Mukai-Transformation
• Sechs Operationen
• Perverse Garbe
• D-Modul
• Beilinson-Bernstein-Lokalisierung
• Modulspektrum
• Semiorthogonale Zerlegung
• Bridgeland Stabilitätsbedingung

Anmerkungen

Verweise

Einige Lehrbucheinführungen in triangulierte Kategorien sind:

• Gelfand, Sergei; Manin, Yuri (2006), "IV. Triangulated Categories", Methoden der homologischen Algebra , Springer-Monographien in der Mathematik (2. Aufl.), Springer-Verlag , doi : 10.1007 / 978-3-662-12492-5 , ISBN   978-3540435839 , MR   1950475
• Kashiwara, Masaki ; Schapira, Pierre (2006), Kategorien und Garben , Grundlehren der mathematischen Wissenschaften, Berlin, New York: Springer-Verlag , doi : 10.1007 / 3-540-27950-4 , ISBN   978-3-540-27949-5 , MR   2182076
• Weibel, Charles A. (1994). Eine Einführung in die homologische Algebra . Cambridge Studies in Advanced Mathematics. 38 . Cambridge University Press. ISBN   978-0-521-55987-4 . MR   1269324 . OCLC   36131259 .

Eine kurze Zusammenfassung der Anwendungen lautet:

• Kashiwara, Masaki ; Schapira, Pierre (2002), "Kapitel I. Homologische Algebra", Garben auf Mannigfaltigkeiten , Grundlehren der mathematischen Wissenschaften, Springer-Verlag , doi : 10.1007 / 978-3-662-02661-8 , ISBN   978-3540518617 , MR   1074006

Einige fortgeschrittenere Referenzen sind:

• Beilinson, AA ; Bernstein, J . ; Deligne, P. (2018) [1982], "Faisceaux pervers" , Astérisque , Société Mathématique de France, Paris, 100 , ISBN   978-2-85629-878-7 , MR   0751966
• Dugger, Daniel; Shipley, Brooke (2009), "Ein merkwürdiges Beispiel für triangulierte äquivalente Modellkategorien, die nicht Quillen-äquivalent sind", Algebraic and Geometric Topology , 9 : 135–166, arXiv : 0710.3070 , doi : 10.2140 / agt.2009.9.135 , MR   2482071
• Hartshorne, Robin (1966), "Kapitel I. Die abgeleitete Kategorie", Residuen und Dualität , Lecture Notes in Mathematics 20 , Springer-Verlag , S. 20–48, doi : 10.1007 / BFb0080482 , ISBN   978-3-540-03603-6 , MR   0222093
• Krause, Henning (2010), "Lokalisierungstheorie für triangulierte Kategorien", Triangulierte Kategorien , Lecture Note Series der London Mathematical Society, 375 , Cambridge University Press, S. 161–235, arXiv : 0806.1324 , doi : 10.1017 / CBO9781139107075.005 , MR   2681709
• Neeman, Amnon (1996), "Der Grothendieck-Dualitätssatz über Bousfields Techniken und Brown-Repräsentierbarkeit", Journal of American Mathematical Society , 9 : 205–236, doi : 10.1090 / S0894-0347-96-00174-9 , MR   1308405
• Neeman, Amnon (2001), Triangulierte Kategorien , Annals of Mathematics Studies, Princeton University Press, doi : 10.1515 / 9781400837212 , ISBN   978-0691086866 , MR   1812507
• Puppe, Dieter (1962), "Zur formalen Struktur der stabilen Homotopietheorie", Kolloquium zur algebraischen Topologie , Aarhus Universitet Matematisk Institute, S. 65–71, Zbl   0139.41106
• Puppe, Dieter (1967), "Stabile Homotopietheorie. I.", Mathematische Annalen , 169 : 243–274, doi : 10.1007 / BF01362348 , MR   0211400
• Ravenel, Douglas (1992), Nilpotenz und Periodizität in der Theorie der stabilen Homotopie , Princeton University Press, ISBN   9780691025728 , MR   1192553
• Rizzardo, Alice; Van den Bergh, Michel ; Neeman, Amnon (2019), "Ein Beispiel eines Nicht-Fourier-Mukai-Funktors zwischen abgeleiteten Kategorien kohärenter Garben", Inventiones Mathematicae , 216 : 927–1004, arXiv : 1410.4039 , doi : 10.1007 / s00222-019-00862-9 , MR   3955712
• Toën, Bertrand (2007), "Die Homotopietheorie der dg-Kategorien und die abgeleitete Morita-Theorie", Inventiones Mathematicae , 167 : 615–667, arXiv : math / 0408337 , doi : 10.1007 / s00222-006-0025-y , MR   2276263
• Verdier, Jean-Louis (1977) [1963], "Catégories dérivées: quelques résultats (état 0)", Cohomologie étale (SGA 4 1/2) (PDF) , Lecture Notes in Mathematics, 569 , Springer, S. 262– 311, doi : 10.1007 / BFb0091525 , ISBN   978-3-540-08066-4 , MR   3727440
• Verdier, Jean-Louis (1996) [1967], Des catégories dérivées des catégories abéliennes , Astérisque, 239 , Société Mathématique de France, MR   1453167

Externe Links

• J. Peter May , Die Axiome für triangulierte Kategorien
• Die Autoren des Stacks-Projekts , The Stacks-Projekt