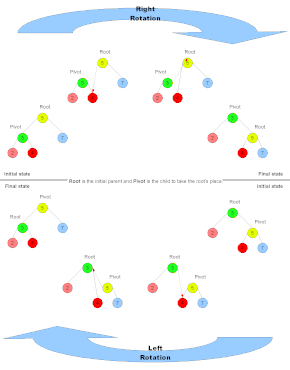
Baumrotation - Tree rotation

Generische Baumrotationen.

In der diskreten Mathematik ist die Baumrotation eine Operation an einem binären Baum , die die Struktur ändert, ohne die Reihenfolge der Elemente zu beeinträchtigen. Eine Baumrotation verschiebt einen Knoten im Baum nach oben und einen Knoten nach unten. Es wird verwendet, um die Form des Baums zu ändern und insbesondere seine Höhe zu verringern, indem kleinere Teilbäume nach unten und größere Teilbäume nach oben verschoben werden, was zu einer verbesserten Leistung vieler Baumoperationen führt.

Hinsichtlich der Definition der Drehrichtung bestehen Unstimmigkeiten in den unterschiedlichen Beschreibungen . Einige sagen, dass die Rotationsrichtung die Richtung widerspiegelt, in die sich ein Knoten bei der Rotation bewegt (ein linker Unterbaum, der sich in die Position seines Elternteils dreht, ist eine Rechtsrotation), während andere sagen, dass die Rotationsrichtung widerspiegelt, welcher Teilbaum sich dreht (ein linker Teilbaum, der sich in die Position seines Elternteils ist eine Linksdrehung, das Gegenteil von ersterem). Dieser Artikel verfolgt den Ansatz der gerichteten Bewegung des rotierenden Knotens.

Illustration

Der rechte Drehvorgang , wie in dem benachbarten Bild gezeigt mit durchgeführt Q als Wurzel und daher ist eine rechte Drehung auf oder an, wurzelte Q . Diese Operation führt zu einer Drehung des Baums im Uhrzeigersinn. Die umgekehrte Operation ist die Linksdrehung, die zu einer Bewegung gegen den Uhrzeigersinn führt (die oben gezeigte Linksdrehung hat ihre Wurzel bei P ). Der Schlüssel zum Verständnis der Funktionsweise einer Rotation besteht darin, ihre Beschränkungen zu verstehen. Insbesondere kann sich die Reihenfolge der Blätter des Baumes (z. B. wenn sie von links nach rechts gelesen wird) nicht ändern (anders kann man sich vorstellen, dass die Reihenfolge, in der die Blätter bei einer Durchquerung in der richtigen Reihenfolge besucht werden, nach dem Betrieb wie bisher). Eine weitere Einschränkung ist die Haupteigenschaft eines binären Suchbaums, nämlich dass das rechte Kind größer als das Elternteil und das linke Kind kleiner als das Elternteil ist. Beachten Sie, dass das rechte Kind eines linken Kindes der Wurzel eines Unterbaums (zum Beispiel Knoten B im Diagramm für den Baum mit Wurzel Q) zum linken Kind der Wurzel werden kann, das selbst das rechte Kind des " new" root im gedrehten Unterbaum, ohne eine dieser Einschränkungen zu verletzen. Wie Sie im Diagramm sehen können, ändert sich die Reihenfolge der Blätter nicht. Die umgekehrte Operation behält ebenfalls die Reihenfolge bei und ist die zweite Art der Drehung.

Angenommen, es handelt sich um einen binären Suchbaum , wie oben erwähnt, müssen die Elemente als miteinander vergleichbare Variablen interpretiert werden. Die alphabetischen Zeichen auf der linken Seite werden als Platzhalter für diese Variablen verwendet. In der Animation rechts werden Großbuchstaben als Platzhalter für Variablen verwendet, während griechische Kleinbuchstaben Platzhalter für einen ganzen Satz von Variablen sind. Die Kreise repräsentieren einzelne Knoten und die Dreiecke repräsentieren Unterbäume. Jeder Unterbaum kann leer sein, aus einem einzelnen Knoten bestehen oder aus einer beliebigen Anzahl von Knoten bestehen.

Detaillierte Abbildung

Bildliche Beschreibung, wie Drehungen gemacht werden.

Wenn ein Unterbaum gedreht wird, erhöht die Unterbaumseite, auf der er gedreht wird, seine Höhe um einen Knoten, während der andere Unterbaum seine Höhe verringert. Dies macht Baumrotationen nützlich, um einen Baum neu auszubalancieren.

Betrachten Sie die Terminologie Root für den Elternknoten der zu drehenden Unterbäume, Pivot für den Knoten, der der neue Elternknoten wird, RS für die Rotationsseite und OS für die gegenüberliegende Rotationsseite. Für die Wurzel Q im obigen Diagramm ist RS C und OS ist P. Mit diesen Begriffen lautet der Pseudocode für die Rotation:

Pivot = Root.OS
Root.OS = Pivot.RS
Pivot.RS = Root
Root = Pivot

Dies ist eine konstante Zeitoperation.

Der Programmierer muss auch sicherstellen, dass das Elternteil der Wurzel nach der Drehung auf den Pivot zeigt. Außerdem sollte der Programmierer beachten, dass diese Operation zu einer neuen Wurzel für den gesamten Baum führen kann und darauf achten, die Zeiger entsprechend zu aktualisieren.

Invarianz

Die Baumrotation macht die Inorder-Traversierung des Binärbaums invariant . Dies bedeutet, dass die Reihenfolge der Elemente nicht beeinflusst wird, wenn eine Drehung in irgendeinem Teil des Baums durchgeführt wird. Hier sind die Inorder-Traversierungen der oben gezeigten Bäume:

Left tree: ((A, P, B), Q, C)        Right tree: (A, P, (B, Q, C))

Das eine aus dem anderen zu berechnen ist sehr einfach. Das Folgende ist ein Python- Beispielcode , der diese Berechnung durchführt:

def right_rotation(treenode):
    """Rotate the specified tree to the right."""
    left, Q, C = treenode
    A, P, B = left
    return (A, P, (B, Q, C))

Eine andere Sichtweise ist:

Rechtsrotation des Knotens Q:

Let P be Q's left child.
Set Q's left child to be P's right child.
[Set P's right-child's parent to Q]
Set P's right child to be Q.
[Set Q's parent to P]

Linksrotation von Knoten P:

Let Q be P's right child.
Set P's right child to be Q's left child.
[Set Q's left-child's parent to P]
Set Q's left child to be P.
[Set P's parent to Q]

Alle anderen Verbindungen bleiben unverändert.

Es gibt auch Doppelrotationen , die Kombinationen von Links- und Rechtsrotationen sind. Eine doppelte Linksdrehung bei X kann als Rechtsdrehung am rechten Kind von X gefolgt von einer Linksdrehung bei X definiert werden; ähnlich kann eine doppelte Rechtsdrehung bei X definiert werden als eine Linksdrehung bei dem linken Kind von X gefolgt von einer Rechtsdrehung bei X.

Baum Drehungen werden in einer Reihe von Baum verwendet Datenstrukturen wie AVL - Bäume , rot-schwarz Bäume , WAVL Bäume , spreizen Bäume und treaps . Sie benötigen nur konstante Zeit, da es sich um lokale Transformationen handelt: Sie arbeiten nur an 5 Knoten und müssen den Rest des Baums nicht untersuchen.

Rotationen zum Rebalancing

Bildliche Beschreibung, wie Rotationen einen Ausgleich in einem AVL-Baum bewirken.

Ein Baum kann durch Rotationen neu ausbalanciert werden. Nach einer Drehung erhöht die Seite der Drehung ihre Höhe um 1, während die der Drehung gegenüberliegende Seite ihre Höhe in ähnlicher Weise verringert. Daher kann man strategisch Rotationen auf Knoten anwenden, deren linkes Kind und rechtes Kind sich in der Höhe um mehr als 1 unterscheiden. Selbstausgleichende binäre Suchbäume wenden diese Operation automatisch an. Ein Baumtyp , der diese Rebalancing - Technik verwendet , ist der AVL - Baum .

Drehabstand

Der Rotationsabstand zwischen zwei beliebigen Binärbäumen mit der gleichen Anzahl von Knoten ist die minimale Anzahl von Rotationen, die erforderlich ist, um einen in den anderen zu transformieren. Mit diesem Abstand wird die Menge der n- Knoten-Binärbäume zu einem metrischen Raum : Der Abstand ist symmetrisch, positiv, wenn zwei verschiedene Bäume gegeben sind, und erfüllt die Dreiecksungleichung .

Es ist ein offenes Problem, ob es einen polynomialen Zeitalgorithmus zur Berechnung des Drehabstands gibt. Der Algorithmus von Fordham berechnet jedoch eine Distanz in linearer Zeit, erlaubt jedoch nur 2 Arten von Drehungen: (ab)c = a(bc) und a((bc)d) = a(b(cd)). Der Algorithmus von Fordham beruht auf einer Klassifizierung von Knoten in 7 Typen, und eine Nachschlagetabelle wird verwendet, um die Anzahl von Umdrehungen zu finden, die erforderlich ist, um einen Knoten eines Typs in einen anderen zu transformieren.

Daniel Sleator , Robert Tarjan und William Thurston zeigten, dass der Rotationsabstand zwischen zwei beliebigen n- Knoten-Bäumen (für n ≥ 11) höchstens 2 n  − 6 beträgt und dass einige Baumpaare so weit auseinander liegen, sobald n ausreichend ist groß. Lionel Pournin zeigte, dass solche Paare tatsächlich immer dann existieren, wenn n ≥ 11.

Siehe auch

• AVL-Baum , Rot-Schwarz-Baum und Spreizbaum , Arten von binären Suchbaum- Datenstrukturen, die Rotationen verwenden, um das Gleichgewicht zu halten.
• Assoziativität einer binären Operation bedeutet, dass die Durchführung einer Baumrotation an ihr das Endergebnis nicht ändert.
• Der Day-Stout-Warren-Algorithmus gleicht einen unausgeglichenen BST aus.
• Tamari-Gitter , eine teilweise geordnete Menge, in der die Elemente als binäre Bäume definiert werden können und die Anordnung zwischen den Elementen durch die Baumrotation definiert wird.

Verweise

Externe Links

• Das AVL Tree Rotations Tutorial (RTF) von John Hargrove